Example 4.3 calculates the step response of the system in Fig. 4-2. Example 4.4 calculates the step response of the same system preceded by a digital filter with the transfer function D(z) = (2 − z⁻¹). This system is shown in Fig. P4.4-1.

Example 4.3

Given the system shown in Fig. 4-2, with input e(t) a unit step function, let us determine the output function C(z). Now,

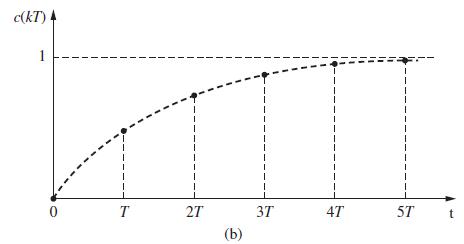
Example 4.4

Let us determine the step response of the system shown in Fig. 4-5. Suppose that the filter is described by the difference equation

Figure 4-5

Transcribed Image Text:

(a) E(s) e(t) T E*(s) e(kT') D(z) 2-z-1 Fig. P4.4-1 Solve for the output of the digital filter M(z) m(kT) 1-8-7's S Gp(s) 3+1 C(s) m(kT). (b) Let the response in Example 4.3 be denoted as c(kT). Use the results in part (a) to express the output c(AT) in Fig. P4.4-1 as a function of q(KT). (c) Use the response (kr) calculated in Example 4.3 and the results in part (b) to find the output c(kr) in Fig. P4.4-1. This result should be the same as in Example 4.4. (d) Use the response C (2) calculated in Example 4.3 and the result in part (b) to find the output C(z) in Fig. P4.4-1. This result should be the same as in Example 4.4.