Consider the half car model in Figure P5.3. The vehicle is traveling with a velocity \(V\) on a sinusoidal road surface with an amplitude of \(0.011 \mathrm{~m}\) and a wavelength of \(5.3 \mathrm{~m}\).

Parameters of the system are as follows: \(\ell_{1}=1.35 \mathrm{~m}, \ell_{2}=\) \(1.05 \mathrm{~m}, I_{c}=1,556 \mathrm{~kg}-\mathrm{m}^{2}, m_{1}=1,010 \mathrm{~kg}, m_{2}=38 \mathrm{~kg}, k_{1}=31,110 \mathrm{~N} / \mathrm{m}\), \(k_{2}=41,310 \mathrm{~N} / \mathrm{m}, \quad k_{3}=321,100 \mathrm{~N} / \mathrm{m}, \quad c_{1}=3,980 \mathrm{~N}-\mathrm{sec} / \mathrm{m}\), and \(c_{2}=\) \(4,980 \mathrm{~N}-\mathrm{sec} / \mathrm{m}\).

Figure P5.3 

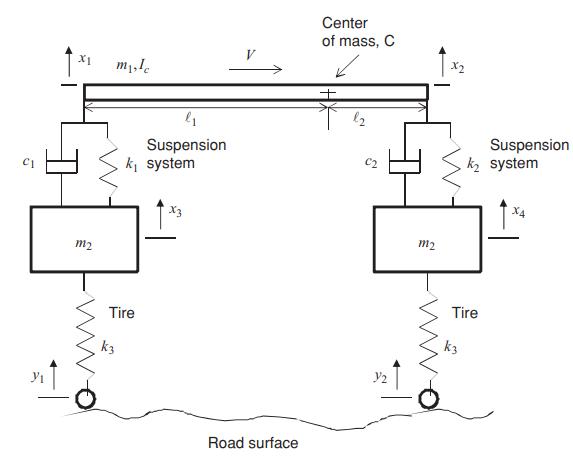
a. Compute the natural frequencies and the mode shapes.

b. Compute the modal damping ratios.

c. Find the critical speed of the vehicle. At the lowest critical speed, compute the steady-state response.

Transcribed Image Text:

15 X1 m,Ic Center of mass, C m2 Suspension k system Tire k3 S Road surface m2 12 Suspension k system Tire k3