A Hausman test based on the difference between fixed effects two-stage least squares and error components two-stage
Question:
A Hausman test based on the difference between fixed effects two-stage least squares and error components two-stage least squares. This is based on Problem 04.1.1 in Econometric Theory by Baltagi (2004). Consider the first structural equation of a simultaneous equation panel data model given in (7.1). Hausman (1978) suggests comparing the FE and RE estimators in the classic panel data regression. With endogenous right-hand-side regressors like \(Y_{1}\) this test can be generalized to test \(H_{0} ; E\left(u_{1} \mid Z_{1}ight)=0\) based on \(\widehat{q}_{1}=\) \(\widetilde{\delta}_{1, F E 2 S L S}-\widehat{\delta}_{1, E C 2 S L S}\) where \(\widetilde{\delta}_{1, F E 2 S L S}\) is defined in (7.6) and \(\widehat{\delta}_{1, E C 2 S L S}\) is defined in (7.11).
(a) Show that under \(H_{0}: E\left(u_{1} \mid Z_{1}ight)=0\), plim \(\widehat{q}_{1}=0\) and the asymptotic cov \(\left(\widehat{q}_{1}, \widehat{\delta}_{1, E C 2 S L S}ight)=0\).
(b) Conclude that \(\operatorname{var}\left(\widehat{q}_{1}ight)=\operatorname{var}\left(\widetilde{\delta}_{1, F E 2 S L S}ight)-\operatorname{var}\left(\widehat{\delta}_{1, E C 2 S L S}ight)\), where var denotes the asymptotic variance. This is used in computing the Hausman test statistic given by \(m_{1}=\hat{q}_{1}^{\prime}\left[\operatorname{var}\left(\widehat{q}_{1}ight)ight]^{-1} \widehat{q}_{1}\). Under \(H_{0}, m_{1}\) is asymptotically distributed as \(\chi_{r}^{2}\), where \(r\) denotes the dimension of the slope vector of the time varying variables in \(Z_{1}\). This can be easily implemented using Stata.
(c) Compute the usual Hausman test based on FE and RE and this alternative Hausman test based on FE2SLS and EC2SLS for the crime data considered in problem 7.11. What do you conclude?
(d) Show that Hausman's test based on the contrast between FE2SLS and EC2SLS can be alternatively obtained from any one of the following artificial 2SLS regressions with instruments \(A=[\tilde{X}, \bar{X}]\) :\[\begin{aligned}& y_{1}^{*}=Z_{1}^{*} \delta_{1}+\tilde{Z}_{1} \gamma_{1}+\omega_{1} \\& y_{1}^{*}=Z_{1}^{*} \delta_{1}+\bar{Z}_{1} \gamma_{1}+\omega_{2} \\& y_{1}^{*}=Z_{1}^{*} \delta_{1}+Z_{1} \gamma_{1}+\omega_{3}\end{aligned}\]Here, \(Z_{1}^{*}=\Omega_{11}^{-1 / 2} Z_{1}, \widetilde{Z}_{1}=Q Z_{1}\), and \(\bar{Z}_{1}=P Z_{1}\), where \(\Omega_{11}^{-1 / 2}\) is defined in (7.16). \(\tilde{X}, \bar{X}\) and \(y^{*}\) are similarly defined; see (7.15). Show that Hausman's test is equivalent to testing whether \(\gamma_{1}=0\) in any one of these three 2SLS regressions; see Baltagi and Liu (2007).
![]()
![]()
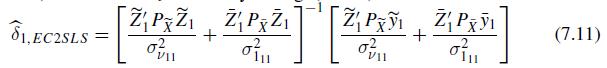
![]()
![]()
Step by Step Answer:






