(a) Verify that (left(partial V_{ho} / partial hoight)_{ho=0}=G=left(partial V_{lambda} / partial lambdaight)_{lambda=0}) where (G) is the bidiagonal...
Question:
(a) Verify that \(\left(\partial V_{ho} / \partial hoight)_{ho=0}=G=\left(\partial V_{\lambda} / \partial \lambdaight)_{\lambda=0}\) where \(G\) is the bidiagonal matrix with bidiagonal elements all equal to one.
(b) Using this result verify that the joint LM statistic given in (5.36) is the same whether the residual disturbances follow an \(\operatorname{AR}(1)\) or an MA(1) process, i.e., the joint LM test statistic for \(H_{1}^{a}: \sigma_{\mu}^{2}=0 ; \lambda=0\) is the same as that for \(H_{1}^{b}\) : \(\sigma_{\mu}^{2}=0 ; ho=0\).
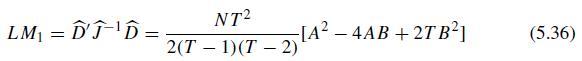
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





