Breusch and Pagan (1980) Lagrange multiplier test. Under normality of the disturbances, show that for the likelihood
Question:
Breusch and Pagan (1980) Lagrange multiplier test. Under normality of the disturbances, show that for the likelihood function given in (4.15),
(a) The information matrix is block-diagonal between \(\theta^{\prime}=\left(\sigma_{\mu}^{2}, \sigma_{\lambda}^{2}, \sigma_{u}^{2}ight)\) and \(\delta\).
(b) For \(H_{0}^{c} ; \sigma_{\mu}^{2}=\sigma_{\lambda}^{2}=0\), verify (4.18), (4.20), and (4.22).
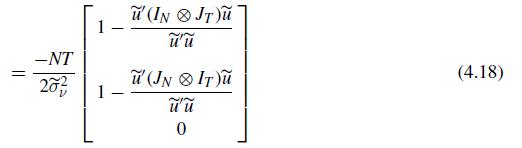
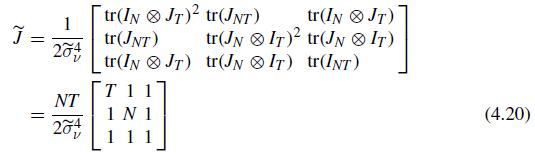
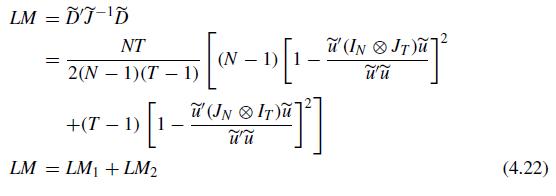
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answered By
Jehal Shah
I believe everyone should try to be strong at logic and have good reading habit. Because If you possess these two skills, no matter what difficult situation is, you will definitely find a perfect solution out of it. While logical ability gives you to understand complex problems and concepts quite easily, reading habit gives you an open mind and holistic approach to see much bigger picture.
So guys, I always try to explain any concept keeping these two points in my mind. So that you will never forget any more importantly get bored.
Last but not the least, I am finance enthusiast. Big fan of Warren buffet for long term focus investing approach. On the same side derivatives is the segment I possess expertise.
If you have any finacne related doubt, do reach me out.
1+ Reviews
10+ Question Solved
Related Book For 
Question Posted:
