Equivalence of several EC3SLS estimators. (a) Prove that (A=left(I_{M} otimes tilde{X}, I_{M} otimesight.) (bar{X})) yields the same
Question:
Equivalence of several EC3SLS estimators.
(a) Prove that \(A=\left(I_{M} \otimes \tilde{X}, I_{M} \otimesight.\) \(\bar{X})\) yields the same projection as \(B=(H \otimes \widetilde{X}, G \otimes \bar{X})\) or \(C=[(H \otimes \widetilde{X}+G \otimes\) \(\bar{X}), H \otimes \tilde{X}]\) or \(D=[H \otimes \widetilde{X}+G \otimes \bar{X}), G \otimes \bar{X}]\) where \(H\) and \(G\) are nonsingular \(M \times M\) matrices (see Baltagi and Li 1992). Conclude that these sets of instruments yield the same EC3SLS estimator of \(\delta\) given by (7.25).
(b) Let \(H=\Sigma_{u}^{-1 / 2}\) and \(G=\Sigma_{1}^{-1 / 2}\), and note that \(\mathrm{A}\) is the set of instruments proposed by Baltagi (1981b) while \(B=\left(\Sigma_{u}^{-1 / 2} \otimes \tilde{X}, \Sigma_{1}^{-1 / 2} \otimes \bar{X}ight)\) is the optimal set of instruments \(X^{*}\) defined (7.30). Conclude that \(H \otimes \widetilde{X}\) is redundant in \(\mathrm{C}\) and \(G \otimes \bar{X}\) is redundant in \(\mathrm{D}\) with respect to the optimal set of instruments \(X^{*}\).
(c) Show that \(P_{A}=P_{I_{M} \otimes \tilde{X}}+P_{I_{M} \otimes \bar{X}}\), and that \(P_{A} P_{B}=P_{B}\) where \(B=\left(\Sigma_{u}^{-1 / 2}ight.\) \(\left.\otimes \tilde{X}, \Sigma_{1}^{-1 / 2} \otimes \bar{X}ight)\). Use this result to prove that the \(\operatorname{avar}\left(\sqrt{n} \hat{\delta}_{E 3 S L S}ight)-\) \(\operatorname{avar}\left(\sqrt{n} \hat{\delta}_{E C 3 S L S}ight)\) is positive semi-definite.
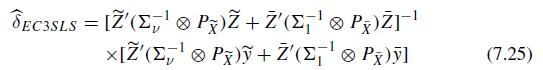
![]()
Step by Step Answer:






