GLS is more efficient than Within. Using the (operatorname{var}left(widehat{beta}_{G L S}ight)) expression below (2.30) and (operatorname{var}left(widetilde{beta}_{W i
Question:
GLS is more efficient than Within. Using the \(\operatorname{var}\left(\widehat{\beta}_{G L S}ight)\) expression below (2.30) and \(\operatorname{var}\left(\widetilde{\beta}_{W i \text { thin }}ight)=\sigma_{v}^{2} W_{X X}^{-1}\), show that
\[\left(\operatorname{var}\left(\widehat{\beta}_{G L S}ight)ight)^{-1}\left(\operatorname{var}\left(\widetilde{\beta}_{\text {Within }}ight)ight)^{-1}=\phi^{2} B_{X X} / \sigma_{v}^{2}\]
which is positive semi-definite. Conclude that \(\operatorname{var}\left(\widetilde{\beta}_{\text {Within }}ight)-\operatorname{var}\left(\widehat{\beta}_{G L S}ight)\) is positive semi-definite.
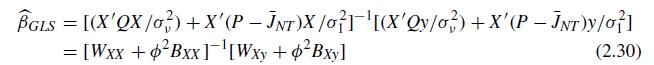
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





