Mundlak's fixed effects result. (a) Using partitioned inverse, show that GLS on (7.35) yields (widehat{beta}_{G L S}=widetilde{beta}_{text
Question:
Mundlak's fixed effects result.
(a) Using partitioned inverse, show that GLS on (7.35) yields \(\widehat{\beta}_{G L S}=\widetilde{\beta}_{\text {Within }}\) and \(\widehat{\pi}_{G L S}=\widehat{\beta}_{\text {Between }}-\widetilde{\beta}_{\text {Within }}\) as given in (7.37) and (7.38).
(b) Verify that \(\operatorname{var}\left(\widehat{\pi}_{G L S}ight)=\operatorname{var}\left(\widehat{\beta}_{\text {Between }}ight)+\operatorname{var}\left(\widetilde{\beta}_{\text {Within }}ight)\) as given in (7.39).
(c) Show that Mundlak's result can also be obtained using system estimation without invoking partitioned inversion. Premultiply (7.35) by \(P\)
\[P y=P X(\beta+\pi)+P \eta\]
Here, we define \(\eta=Z_{\mu} \epsilon+u\), and we use the fact that \(P^{2}=P\) and \(P Z_{\mu}=Z_{\mu}\). Note that OLS or GLS on this equation yields \((\widehat{\beta+\pi})=\left(X^{\prime} P Xight)^{-1} X^{\prime} P y\) which is the Between estimator. Similarly, premultiplying (7.35) by \(Q\) one gets \[Q y=Q X \beta+Q u\]
since \(Q P=0\). OLS or GLS on this equation yields \(\widetilde{\beta}_{\text {Within }}=\left(X^{\prime} Q Xight)^{-1} X^{\prime} Q y\) which is the usual Within or Fixed Effects estimator. Stacking the system of equations, we get \[\left(\begin{array}{l}P y \\Q y\end{array}ight)=\left(\begin{array}{c}P X \\Q X\end{array}ight) \beta+\left(\begin{array}{c}P X \\0\end{array}ight) \pi+\left(\begin{array}{c}
P \eta \\Q u\end{array}ight)\]and the system error vector has mean 0 and variance-covariance matrix given by\[\Sigma=\left(\begin{array}{cc}\sigma_{1}^{2} P & 0 \\0 & \sigma_{u}^{2} Q \end{array}ight)\]
Show that OLS or GLS on this system yields the same results that Mundlak found by applying GLS to (7.35).
(d) Prove that the Zyskind (1967) necessary and sufficient condition for OLS to be equivalent to GLS on the system of equations given in part
(c) is satisfied. This calls for \(P_{Z} \Sigma=\Sigma P_{Z}\), where \(Z=\left(\begin{array}{cc}P X & P X \\ Q X & 0\end{array}ight)\) is the matrix of regressors and \(\Sigma\) is the variance-covariance matrix of its disturbances. See the solution in Baltagi (2006b).
(e) Show that Mundlak's (1978) result could have been obtained with OLS rather than GLS on (7.35). Prove that Zyskind's (1967) necessary and sufficient condition for OLS to be equivalent to GLS holds for (7.35). (Hint: rewrite \(X\) as \((P+Q) X\) in (7.35) and collect like terms before applying OLS).
![]()
![]()
![]()
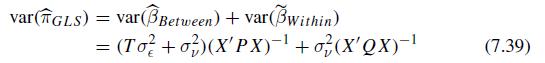
Step by Step Answer:






