Consider the regression model (Y_{t}=beta_{0}+beta_{1} X_{t}+u_{t}), where (u_{t}) follows the stationary (mathrm{AR}(1)) model (u_{t}=phi_{1} u_{t-1}+widetilde{u}_{t}) with (widetilde{u}_{t})
Question:
Consider the regression model \(Y_{t}=\beta_{0}+\beta_{1} X_{t}+u_{t}\), where \(u_{t}\) follows the stationary \(\mathrm{AR}(1)\) model \(u_{t}=\phi_{1} u_{t-1}+\widetilde{u}_{t}\) with \(\widetilde{u}_{t}\) i.i.d. with mean 0 and variance \(\sigma_{\tilde{u}}^{2}\) and \(\left|\phi_{1}\right|
a. Show that \(\operatorname{var}\left(u_{t}\right)=\frac{\sigma_{\tilde{u}}^{2}}{1-\phi_{1}^{2}}\) and \(\operatorname{var}\left(X_{t}\right)=\frac{\sigma_{e}^{2}}{1-\gamma_{1}^{2}}\).
b. Show that \(\operatorname{cov}\left(u_{t}, u_{t-j}\right)=\phi_{1}^{j} \operatorname{var}\left(u_{t}\right)\) and \(\operatorname{cov}\left(X_{t}, X_{t-j}\right)=\gamma_{1}^{j} \operatorname{var}\left(X_{t}\right)\).
c. Show that \(\operatorname{corr}\left(u_{t}, u_{t-j}\right)=\phi_{1}^{j}\) and \(\operatorname{corr}\left(X_{t}, X_{t-j}\right)=\gamma_{1}^{j}\).
d. Consider the terms \(\sigma_{v}^{2}\) and \(f_{T}\) in Equation (16.14).
i. Show that \(\sigma_{v}^{2}=\sigma_{X}^{2} \sigma_{u}^{2}\), where \(\sigma_{X}^{2}\) is the variance of \(X\) and \(\sigma_{u}^{2}\) is the variance of \(u\).
ii. Derive an expression for \(f_{\infty}\).
Equation (16.14)
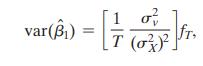
Step by Step Answer:






