Derive Equation (16.7) from Equation (16.4), and show that (delta_{0}=beta_{0}), (delta_{1}=beta_{1}, delta_{2}=beta_{1}+beta_{2}, delta_{3}=beta_{1}+beta_{2}+beta_{3}) (etc.). Note that (X_{t}=Delta
Question:
Derive Equation (16.7) from Equation (16.4), and show that \(\delta_{0}=\beta_{0}\), \(\delta_{1}=\beta_{1}, \delta_{2}=\beta_{1}+\beta_{2}, \delta_{3}=\beta_{1}+\beta_{2}+\beta_{3}\) (etc.). Note that \(X_{t}=\Delta X_{t}+\) \(\Delta X_{t-1}+\cdots+\Delta X_{t-p+1}+X_{t-p}\).
Equation (16.7)
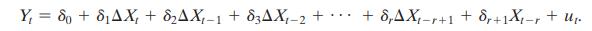
Equation (16.4)
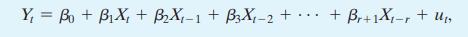
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





