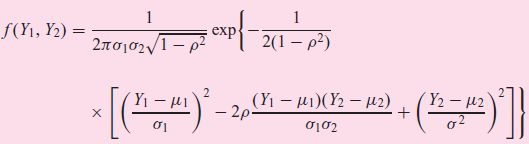If two random variables are statistically independent, the coefficient of correlation between the two is zero. But the converse is not necessarily true; that is,

€œIf two random variables are statistically independent, the coefficient of correlation between the two is zero. But the converse is not necessarily true; that is, zero correlation does not imply statistical independence. However, if two variables are normally distributed, zero correlation necessarily implies statistical independence.€ Verify this statement for the following joint probability density function of two normally distributed variables Y₁and Y₂(this joint probability density function is known as the bivariate normal probability density function):

For a general discussion of the properties of the maximum likelihood estimators as well as for the distinction between asymptotic unbiasedness and consistency. Roughly speaking, in asymptotic unbiasedness we try to find out the lim E (σ̃n² ) as n tends to infinity, where n is the sample size on which the estimator is based, whereas in consistency we try to find out how σ̃n² behaves as n increases indefinitely. Notice that the unbiasedness property is a repeated sampling property of an estimator based on a sample of given size, whereas in consistency we are concerned with the behavior of an estimator as the sample size increases indefinitely.

where μ₁ = mean of Y₁

μ₂ = mean of Y₂

σ₁ = standard deviation of Y₁

σ₂ = standard deviation of Y₂

ρ = coefficient of correlation between Y₁ and Y₂

F(Y1, Y2) = exp 2(1 p2) : ? 22 ( i- )(%- ) - 2- -