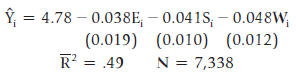In an effort to explain regional wage differentials, you collect wage data from 7,338 unskilled workers, divide the country into four regions (Northeast, South, Midwest, and West), and estimate the following equation (standard errors in parentheses):

Where:

Y_i = the hourly wage (in dollars) of the ith unskilled worker

E_i = a dummy variable equal to 1 if the ith worker lives in the Northeast, 0 otherwise

S_i = a dummy variable equal to 1 if the ith worker lives in the South, 0 otherwise

W_i = a dummy variable equal to 1 if the ith worker lives in the West, 0 otherwise

a. What is the omitted condition in this equation?

b. If you add a dummy variable for the omitted condition to the equation without dropping E_i, S_i, or W_i, what will happen?

c. If you add a dummy variable for the omitted condition to the equation and drop E_i, what will the sign of the new variable€™s estimated coefficient be?

d. Which of the following three statements is most correct? Least correct?

Explain your answers.

i. The equation explains 49 percent of the variation of Y around its mean with regional variables alone, so there must be quite a bit of wage variation by region.

ii. The coefficients of the regional variables are virtually identical, so there must not be much wage variation by region.

iii. The coefficients of the regional variables are quite small compared with the average wage, so there must not be much wage variation by region.

Transcribed Image Text:

Î = 4.78 – 0.038E, – 0.041S, – 0.048W, (0.019) (0.010) (0.012) R? = .49 N = 7,338