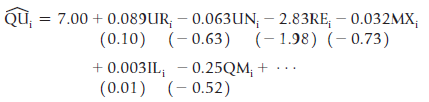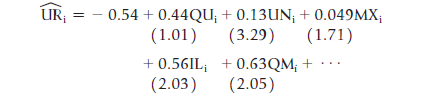Simultaneous equations make sense in cross-sectional as well as time-series applications. For example, James Ragan examined the effects of unemployment insurance (hereafter UI) eligibility standards on unemployment rates and the rate at which workers quit their jobs. Ragan used a pooled data set that contained observations from a number of different states from four different years (requirements for UI eligibility differ by state). His results are as follows (t-scores in parentheses):

Where:

QU_i = the quit rate (quits per 100 employees) in the ith state

UR_i = the unemployment rate in the ith state

UN_i = union membership as a percentage of nonagricultural employment in the ith state

RE_i = average hourly earnings in the ith state relative to the average hourly earnings for the United States

IL_i = dummy variable equal to 1 if workers in the ith state are eligible for UI if they are forced to quit a job because of illness, 0 otherwise

QM_i = dummy variable equal to 1 if the ith state maintains full UI benefits for the quitter (rather than lowering benefits), 0 otherwise

MX_i = maximum weekly UI benefits relative to average hourly earnings in the ith state

a. Hypothesize the expected signs for the coefficients of each of the explanatory variables in the system. Use economic theory to justify your answers. Which estimated coefficients are different from your expectations?

b. Ragan felt that these two equations would encounter simultaneity bias if they were estimated with OLS. Do you agree? Explain your answer.

c. The actual equations included a number of variables not documented earlier, but the only predetermined variable in the system that was included in the QU equation but not the UR equation was RE. What does this information tell you about the identification properties of the QU equation? The UR equation?

d. What are the implications of the lack of significance of the endogenous variables where they appear on the right-hand side of the equations?

e. What, if any, policy recommendations do these results suggest?

Transcribed Image Text:

7.00 + 0.089UR; – 0.063UN; – 2.83RE; – 0.032MX; (0.10) (- 0.63) (-1,98) (- 0.73) + 0.003IL; (0.01) (- 0.52) QU, 0.25QM; + UR; = - 0.54 + 0.44QU; + 0.13UN; + 0.049MX; %3D (3.29) (1.71) + 0.56IL, + 0.63QM; + (1.01) (2.03) (2.05)