Consider the case of a nonlinear elastic material, and extend Exercise 6.8 for the case where the
Question:
Consider the case of a nonlinear elastic material, and extend Exercise 6.8 for the case where the strain energy depends on three invariants of the strain tensor U = U(I1e, I2e, I3e), where:

Note that this new choice of invariants does not change any fundamental aspects of the problem.
Show that using the form σij = ∂U/∂eij and employing the chain rule, yields the nonlinear relation σij = ∅1δij + ∅2eij + ∅3eikejk where ∅i = ∅i(Ije) = ∂U/∂Iie. This type of theory is often referred to as physically nonlinear elasticity in that the constitutive form retains the small deformation strain tensor but includes higher order nonlinear behavior in the constitutive law; see Evans and Pister (1966) and Bharatha and Levinson (1977).
Data from exercise 6.8
In light of Exercise 6.2, consider the formulation where the strain energy is assumed to be a function of the two invariants U = U (Ie, IIe). Show that using the relation σij = ∂U/∂eij and employing the chain rule, yields the expected constitutive law (4.2.7).
Equation 4.2 .7
![]()
Data from exercise 6.2
Since the strain energy has physical meaning that is independent of the choice of coordinate axes, it must be invariant to all coordinate transformations. Because U is a quadratic form in the strains or stresses, it cannot depend on the third invariants IIIe or I3, and so it must depend only on the first two invariants of the strain or stress tensors. Show that the strain energy can be written in the following forms:
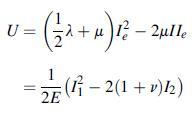
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





