Consider the Papkovich representation for the two dimensional plane strain case where A A 1 (x,y)e 1 A 2 (x,y) e 2 and B B(x,y) Show that this representation will lead to the complex variable formulation 2u(u iv) Ky (2) ZY'(z) Y(2) with appropriate definitions of y(z) and (z) ...

Two Dimensiona 1 Papkovich Representation 2u1 AVB where A A xye Ax ye and B B ...

Consider the Papkovich representation for the two-dimensional plane strain case where A = A 1 (x,y)e 1

Question:

Consider the Papkovich representation for the two-dimensional plane strain case where A = A₁(x,y)e₁ + A₂(x,y) e₂ and B = B(x,y). Show that this representation will lead to the complex variable formulation:

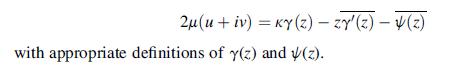
2u(u +iv) - Ky (2) - ZY'(z) - Y(2) with appropriate definitions of y(z) and (z).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books

Question Posted: Jan 15, 2024 05:03 AM

See More Questions

Consider an Exponential random variable X with parameter > 0. Is it always true that, if a and b are positive constants, then Y = aX + b is an Exponential random variable too? If your answer is...
The two vectors A and B are drawn from a common point, and C = 1 + B. (a) Show that if C2 = A2 + B2, the angle between the vectors A and B is 90. (b) Show that if C2 < A2 + B2, the angle between the...
Explain the relationship between three Statement objects, and illustrate why and how the CallableStatement object can use the setXXX() methods defined in the PreparedStatement interface.
In the Olympiad of 708B.C, some athletes competing in the standing long jump used handheld weights called halters to lengthen their jumps (Figure). The weights were swung up in front just before...
What kinds of knowledge does the auditor gather to understand internal control and assess the risk of material misstatement?
5. Supervisor Lisa Kitzinger is interviewing candidates to add a social media expert to her sales team. Kitzinger works in a cubicle, and she has an assistant who could help during the interview...
Sandy Smith, managing director of the Calgary Consulting Group, is examining how overhead costs behave with changes in monthly professional labour- hours billed to clients. Assume the following...
Apollonia Dental Services is part of an HMO that operates in a large metropolitan area. Currently, Apollonia has its own dental laboratory to produce two varieties of porcelain crownsall porcelain...
Show that Kelvins problem of Fig. 13.1 may be solved using the axisymmetric Papkovich functions (Boussinesq potentials): Fig 13.1 Equation 13.3.10 P 2 TR Verify that the displacements match those...
Consider an elastic half-space with z = 0 on the surface z = 0. For the axisymmetric problem, show that the Boussinesq potentials must satisfy the relation A z = 2B/z within the half-space.
A 2005 Harris Interactive for Korbel poll found that 63% of men and 55% of women think that it is okay for women to make marriage proposals to men. An 8% difference may or may not be statistically...
What is a transistor, and what are its types?
Discuss the emerging role of nanotechnology in electrical engineering, focusing on its applications in enhancing electrical components like batteries, supercapacitors, and sensors.Explore the...
1. As resistors are added in parallel to an existing circuit, what happens to the voltage drop measured across each resistor? 2. In the circuit shown on the right, which path (left or right) will...
On the following graphs, identify points where a. The function is not continuous, b. The function is not differentiable (and say why), c. The derivative is zero (critical points). 2 0
Element compound homogeneous mixture (heterogeneous mixture) 4) A piece of gold has a mass of 49.75 g. What should the volume be if it is pure gold? Gold has a density of 19.3 g/cm (3 points) D=m/v...
Engineers must be able to predict the rate of heat loss through a building wall to determine the heating system requirements. They do this by using the concept of thermal resistance R, which relates...
Use the averaging principle developed in Problem 9 to find the temperature distribution of the plate shown in Figure P10, using the 3 3 grid and the given values T a = 150C and T b = 20C. Figure P10...
Solve the following equations: 7x + 9y 9z = 22 + 2y 4z = 12 + 5 z %3D -2 Z.
1. (A nice inharitage) Suppose $1 were invested in 1776 at 3.3% interest compounded yearly a) Approximatelly how much would that investment be worth today: $1,000, $10,000, $100,000, or $1,000,000?...
Why Should not the government subsidize home buyers who make less than $120K per year. please explain this statement
Entries for equity investments: 20%50% ownership On January 6, 20Y8, Bulldog Co. purchased 25% of the outstanding common stock of $159,000. Gator Co. paid total dividends of $20,700 to all...

Consider the Papkovich representation for the two-dimensional plane strain case where A = A 1 (x,y)e 1

Question:

2u(u + iv) = Ky (2) - ZY'(z) - Y(2) with appropriate definitions of y(z) and (z).

Step by Step Answer:

Two Dimensiona 1 Papkovich Representation 2u1 AVB where A A xye Ax ye and B B...View the full answer

Elasticity Theory Applications And Numerics

Students also viewed these Engineering questions