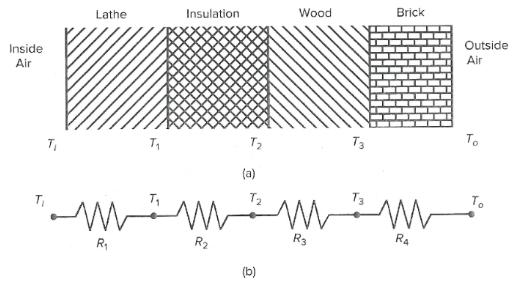
Engineers must be able to predict the rate of heat loss through a building wall to determine the heating system requirements. They do this by using the concept of thermal resistance R, which relates the heat flow rate q through a material to the temperature difference /T across the material: q= ΔT/R. This relation is like the voltage-current relation for an electric resistor: i = v/R. So the heat flow rate plays the role of electric current, and the temperature difference plays the role of the voltage difference. The SI unit for q is the watt (W), which is 1 joule/second (J/s). The wall shown in Figure P8 consists of four layers: an inner layer of plaster/lathe 10 mm thick, a layer of fiber glass insulation 125 mm thick, a layer of wood 60 mm thick, and an outer layer of brick 50 mm thick. If we assume that the inner and outer temperatures T_i and T_o have remained constant for some time, then the heat energy stored in the layers is constant, and thus the heat flow rate through each layer is the same.

Applying conservation of energy gives the following equations.

The thermal resistance of a solid material is given by R = D/k, where D is the material thickness and k is the material’s thermal conductivity. For the given materials, the resistances for a wall area of 1 m² are R₁ = 0.036, R₂ = 4.01, R₃ = 0.408, and R₄ = 0.038 K/W.

Suppose that T_i = 20.C and To"$10.C. Find the other three temperatures and the heat loss rate q, in watts. Compute the heat loss rate if the wall’s area is 10 m₂.

Figure P8