Consider the problem of a concentrated force acting normal to the free surface of a semi-infinite solid
Question:
Consider the problem of a concentrated force acting normal to the free surface of a semi-infinite solid as shown in case: (a) of the following figure. The two-dimensional stress field for this problem is given by equations (8.4.36) as:
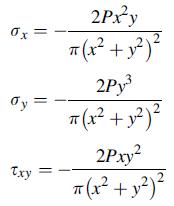
Equation 8.4.36
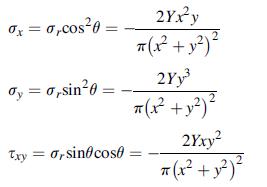
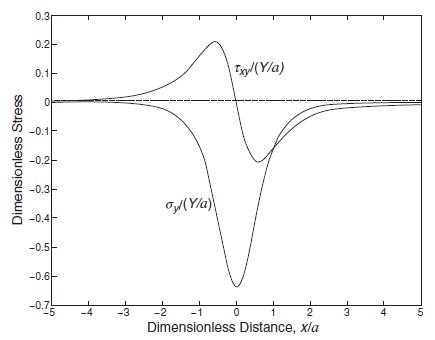
Using this solution with the method of superposition, solve the problem with two concentrated forces as shown in case (b). Because problems(a) and (b) have the same resultant boundary loading, explicitly show that at distances far away from the loading points the stress fields for each case give approximately the same values. Explicitly plot and compare σy and τxy for each problem on the surface y = 10a and y = 100a (see Fig.8.20).
Fig 8.20
a.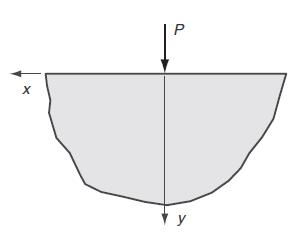
b. 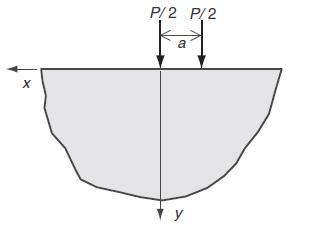
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





