FREE Trial

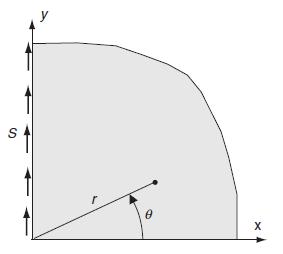
Consider the quarter plane domain problem shown in Fig. 8.17 but this time with a uniformly distributed

Question:

Consider the quarter plane domain problem shown in Fig. 8.17 but this time with a uniformly distributed normal loading N along the y-axis in the x-direction. Use the proposed general Airy function (8.4.19), and apply four proper boundary conditions to determine the unknown constants. Develop the stress solution and similar to Example 8.4.4, and explore the conditions at the corner (x = y = 0).

Fig 8.17

S 0 X

Equation 8.4.19

$=2(a2 +960 + a21 cos 20 + b21 sin 20)

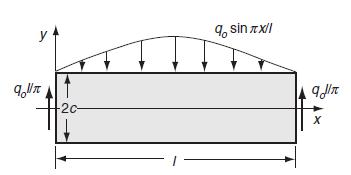
Data from example 8.4.4

Consider the simply supported beam carrying a sinusoidal loading along its top edge as shown in Fig. 8.6. The

Note that these conditions do not specify the pointwise distribution of shear stress on the ends of the beam,

y q* -2c q sinxx/l 9Jr X

Condition (8.2.8)2 implies that [A cosh By + C(By cosh By+sinh y) + B sinh By+D(By sinh By+cosh 6y)]y-tc = 0

while condition (8.2.8)4 gives [c sinh c cosh c cosh Bc (8.2.16) In order for relation (8.2.16) to be truedeveloped through integration of the plane stress strain-displacement relations. Skipping the de- tails, the

These conditions determine the rigid-body terms, giving the result Wo = Vo = 0, Up = [B(1 + v) +2C] (8.2.21)

Transcribed Image Text:

S 0 X

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Answer rating: 0% (1 review)

New boundary conditions for quarter plane problem 0 10T 10 00r 2 N Te ...View the full answer


answer-question
Answered By
tutor-profile-image
David Muchemi
I am a professional academic writer with considerable experience in writing business and economic related papers. I have been writing for my clients who reach out to me personally after being recommended to me by satisfied clients. I have the English language prowess, no grammatical and spelling errors can be found in my work. I double-check for such mistakes before submitting my papers. I deliver finished work within the stipulated time and without fail. I am a good researcher on any topic especially those perceived to be tough. I am ready to work on your papers and ensure you receive the highest quality you are looking for. Please hire me to offer my readily available quality service. Best regards,
4.60+ 27+ Reviews 61+ Question Solved
Related Book For  answer-question
Elasticity Theory Applications And Numerics

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books
Question Posted:
See More Questions

Students also viewed these Engineering questions

The Resume Catalog 200 Damn Good Examples 1st Edition - ISBN: 0898158915 - Free Book