Consider the second order stress tensor representation ij = ,kk ij , ij ,

Consider the second order stress tensor representation σ_ij = ∅_,kkδ_ij –∅,_ij, where∅is a proposed stress function. First show that this scheme gives a divergence-less stress; i.e. σ_ij,j = 0. Next using this representation in the general compatibility equations (5.3.3) with no body forces gives the result:

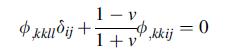
Finally show that for the two-dimensional plane stress case, this representation reduces to the ordinary Airy form from Section 7.5.

Equation 5.3.3

Data from section 7.5

Transcribed Image Text:

ij + 1 - v 1+v ,kkij = 0