Consider the torsion of a rod with the half-ring cross-section as shown. Formulating the problem in polar coordinates (see Exercise 9.6), the governing stress function equation becomes:

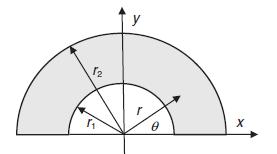
Data from exercise 9.6

We wish to reformulate the torsion problem using cylindrical coordinates. First show that the general form of the displacements can be expressed as u_r = 0, u_θ = αrz, u_z = u_z(r,θ). Next show that this leads to the following strain and stress fields:

Transcribed Image Text:

-2 Using Fourier methods to solve this problem, first show that we can expand the constant right- hand side in a Fourier since series to get -2a =--08ua/[(2n+1)r]sin(2n +1)0. Based on this, use the series solution from (r, 0) = no Fn (r)sin (2n+1)0 and show that the gov- erning equation leads to the ordinary differential equation dFn, 1 dFn (2n + 1), -Fn dr r dr p2 Show that the solution to this equation to give by Fn=An+1+Br -2n-1 +Kr, where Kn Trz 2 1 18 + ar rr a0 Tez 1 d r 30 Note that the stress function form already satisfies the zero boundary condition on 0 = 0 and 7. Finally apply the remaining boundary conditions on r and r2, to determine the constants A,, and Bn and show that the stresses can be written as - ap r |Amr2n + Br n=0 = 2n-2 8 (2n + 1) 8 (2n + 1) (2n-1) (2n + 3) + Knr] (2n + 1) cos(2n + 1)0 -2n-2 An (2n +1)rn - Bn (2n +1)r +2Knr] Sin(2n +1)0 n=0