Determine the components of the vector bi and matrix aij given in Exercise 1.1 in a new
Question:
Determine the components of the vector bi and matrix aij given in Exercise 1.1 in a new coordinate system found through a rotation of 45° (π/4 radians) about the x1-axis. The rotation direction follows the positive sense presented in Example 1.2.
Data from exercise 1.1
For the given matrix/vector pairs, compute the following quantities: aii, aijaij, aijajk, aijbj, aijbibj, bibj, bibi. For each case, point out whether the result is a scalar, vector or matrix. Note that aijbj is actually the matrix product [a]{b}, while aijajk is the product [a][a].
Example 1.2

Fig 1.2
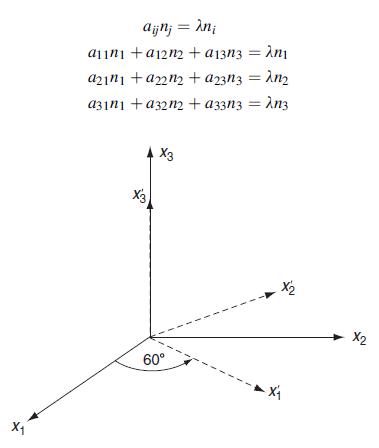

![where [] indicates transpose (defined in Section 1.7). Although simple transformations can be worked out by](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/8/0/1/752659d35d8e34f11704801752710.jpg)
Equation 1.5.1

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.
Question Posted:





