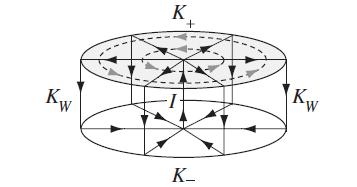
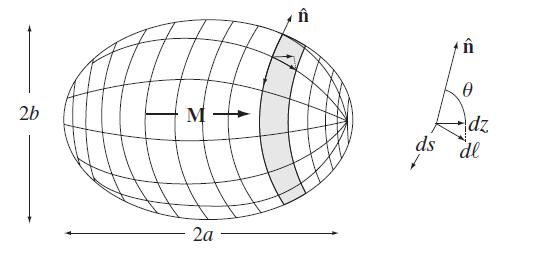
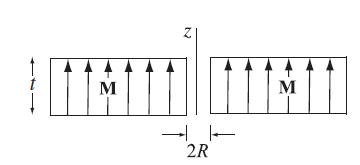
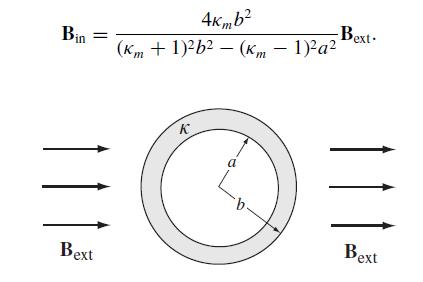
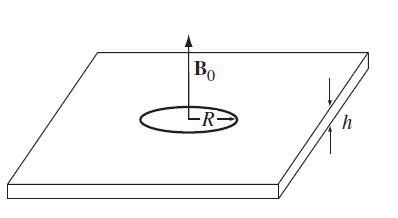
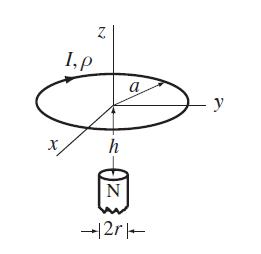
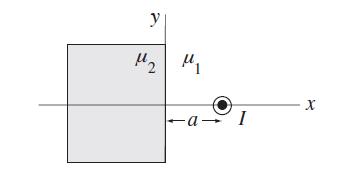
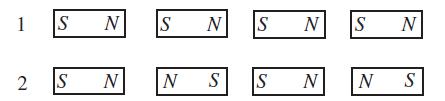
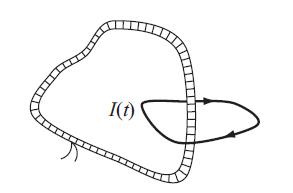
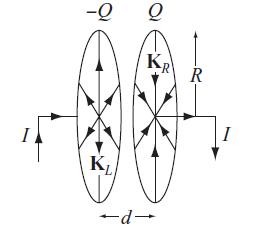
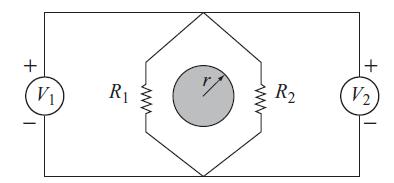
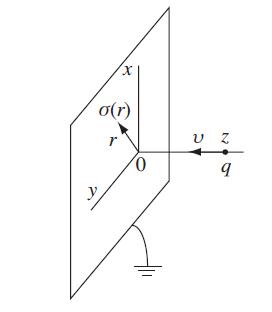
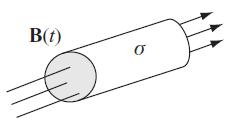
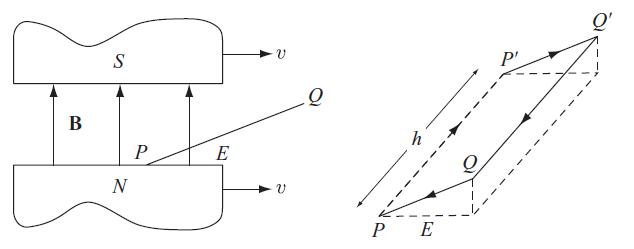
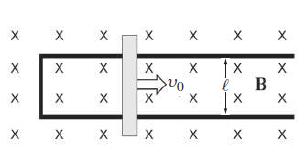
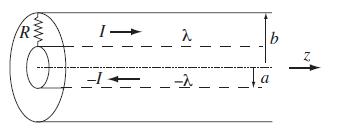
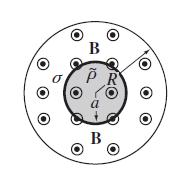
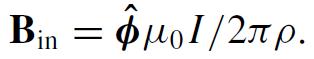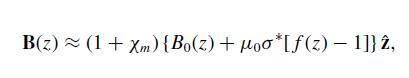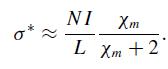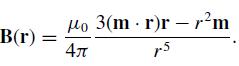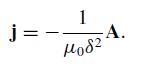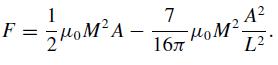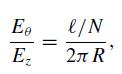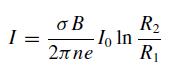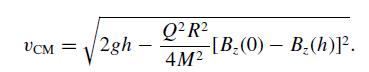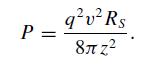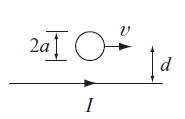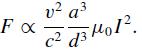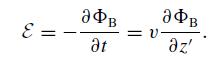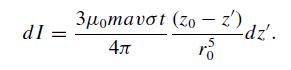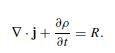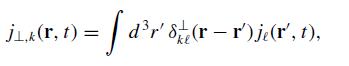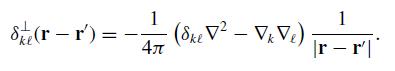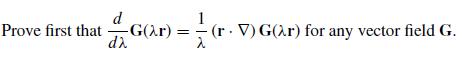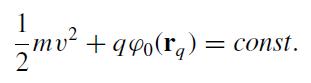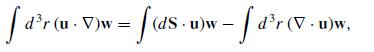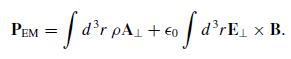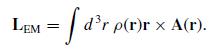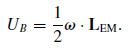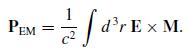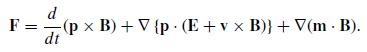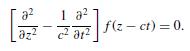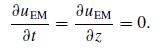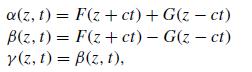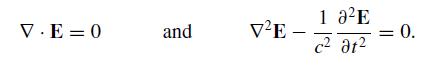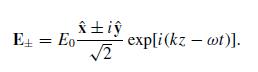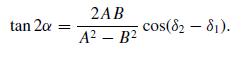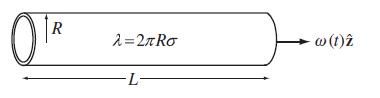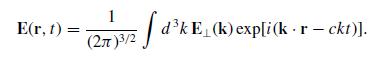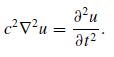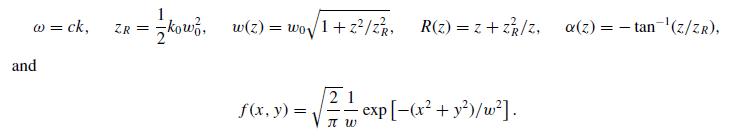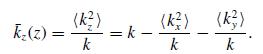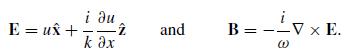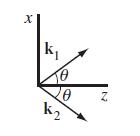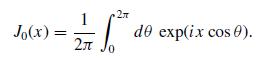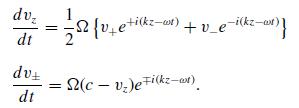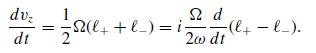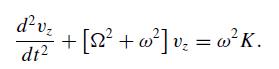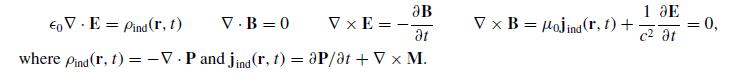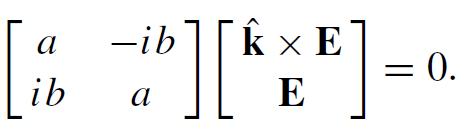Modern Electrodynamics 1st Edition Andrew Zangwill - Solutions

Discover comprehensive solutions with our expertly crafted answers to "Modern Electrodynamics 1st Edition" by Andrew Zangwill. Access step-by-step answers and the complete solution manual online, providing detailed chapter solutions and solved problems. Enhance your learning experience with our instructor manual and test bank, offering a thorough understanding of complex concepts. Our answers key and solutions PDF are available for free download, ensuring you have the essential tools to excel in your studies. Dive into textbook questions and answers, and empower your knowledge with our tailored resources.