Einstein published the following argument in 1910. The solid lines with arrows in the figure below show the directions of current flow for a “can-of-current”. A constant current I flows up the central z-axis of a hollow cylindrical can of radius R, flows radially outward on the top end-cap with surface density K₊, flows down the can side wall with surface density K_W, and then flows radially inward on the bottom end-cap with surface density K₋. In Example 10.2, we used Amp`ere’s law to show that the magnetic field outside the can is zero while the field inside the can is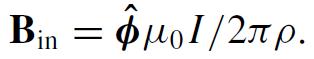

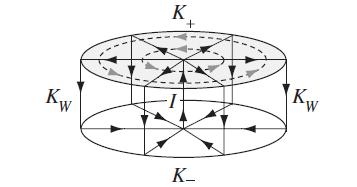
(a) Let the top end-cap carry a magnetization M = M ɸ̂  as indicated by the gray shading and the dashed lines with arrows. According to the text, this magnetization produces H = 0 everywhere so B_M = μ₀M everywhere. Show that B_M exerts a Lorentz force on the end cap which tends to levitate the can. Since the can cannot exert a force on itself, Einstein argued that the Lorentz force density j × B was incorrect and should be replaced by j × H.
(b) Let the magnetized end-cap have a tiny thickness. Calculate and sketch the closed lines of magnetization current density.
(c) Use the sketch from part (b) to identify the part of the end-cap magnetization current that feels a force due to B_in in the zero-thickness limit. Show that this force cancels the levitation force calculated in part (a).

B = quo1/2. Bin