Consider transverse plane waves in free space where E = E(z, t) and B = B(z, t).
Question:
Consider transverse plane waves in free space where E = E(z, t) and B = B(z, t).
(a) Demand that the Poynting vector S = 0 and show that all such solutions must satisfy
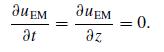
(b) The constancy of uEM implies that the fields can be parameterized as
where α, β, and γ are functions of z and t. In particular, show that S = 0 implies that
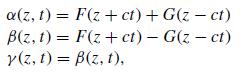
where F(x) and G(x) are arbitrary scalar functions.
(c) Let F = 1 2 k(z + ct) and G = ±1 2 k(z − ct) where ω = ck . For both choices of sign, sketch a snapshot of the fields as a function of z which clearly shows their behavior.
Explain why one of these cases corresponds to the superposition of two counter-propagating, circularly polarized waves.
(d) Sketch the fields as above for F = 1 / 2 k(z + ct) and G = 0.
Step by Step Answer:
b c d Since E E2 t and V E 0 we know that Ezaz 0 Therefore Ez By ...View the full answer
