The function is a beam-like solution to the scalar wave equation (in the paraxial approximation) where The Gouy phase, (z), arises from the fact that

The function

is a beam-like solution to the scalar wave equation (in the paraxial approximation) where

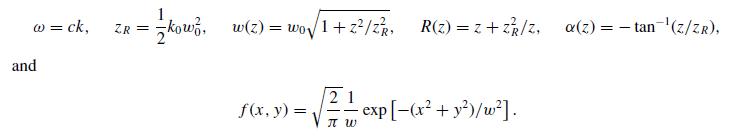
The Gouy phase, α(z), arises from the fact that the beam has a finite size in the transverse direction. To see this, use the fact that k² = k²_x + k²_y + k²_z to motivate the definition of an effective propagation “constant”

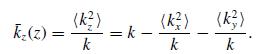
In this formula, the averages are defined over the distribution of transverse wave vectors that make up the beam. That is,

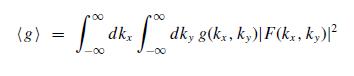
where

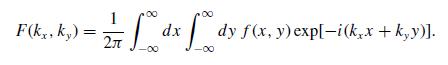
Show that kz + α(z) = ∫₀^z dz k̅_z . Confirm that α(z) = 0 if there is no localization in the transverse direction.

(p. z) = f(x, y) exp[i (kz - wt + kop/2R+ a)]