The angular velocity (t)z of the cylindrical shell shown below increases from zero and smoothly approaches the steady value 0 . The shell has

The angular velocity ω(t)ẑ of the cylindrical shell shown below increases from zero and smoothly approaches the steady value ω₀. The shell has infinitesimal thickness and carries a uniform charge per unit length λ = 2πRσ, where σ is a uniform charge per unit area. Assume that the shell radius R

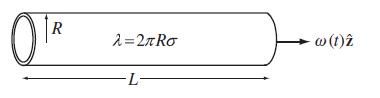
(a) Find the static electric field and steady magnetic field when ω = ω₀.
(b) Find B(r, t) everywhere during the spin-up and use it to find the time-dependent part of the electric field.

(c) The spin-up is performed by an external agent who supplies power at a rate −j · E per unit volume to create the magnetic field. Confirm this by evaluating Poynting’s theorem over all of space. Comment on the role of the Poynting vector and the electric field in this calculation.
(d) Evaluate Poynting’s theorem using a cylindrical volume with a radius slightly smaller than the shell to study the flow of energy into the interior from the surface of the shell.

R 012 = 2Ro -L- w (1) 2