Exercise 8.2 provides the plane stress (see Exercise 3.5 ) solution for a cantilever beam of unit thickness, with depth 2c, and carrying an end load of P with stresses given by:

Data from exercise 3.5

A two-dimensional state of plane stress in the x, y-plane is defined by σ_z = τ _yz = τ _zx = 0. Using general principal value theory, show that for this case the in-plane principal stresses and maximum shear stress are given by:

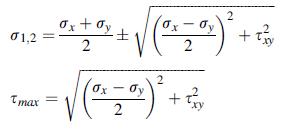
Data from exercise 8.2

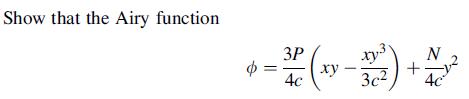
solves the following cantilever beam problem, as shown in the following figure. As usual for such problems, boundary conditions at the ends (x = 0 and L) should be formulated only in terms of the resultant force system, while at y = ± c the exact pointwise specification should be used. For the case with N = 0, compare the elasticity stress field with the corresponding results from strength of materials theory.

Transcribed Image Text:

3P 203 Show that the principal stresses are given by 1,2 = xy v (c y) + xy 3P 4c3 0x xy, dy = 0, and the principal directions are Txy 3P 4c = n (1,2) 12) = [(xy (e 3) + x3 ) + (2 y)ez] - - Note that the principal directions do not depend on the loading P. X constant