For Example 16.1, show that the element stiffness equations for the isotropic case are given by relations (16.4.1) and (16.4.2).

Data from example 16.1

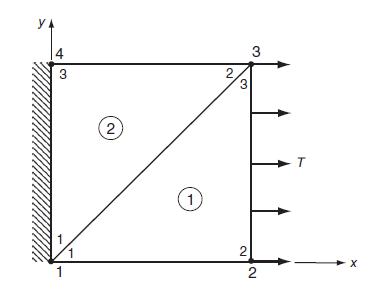
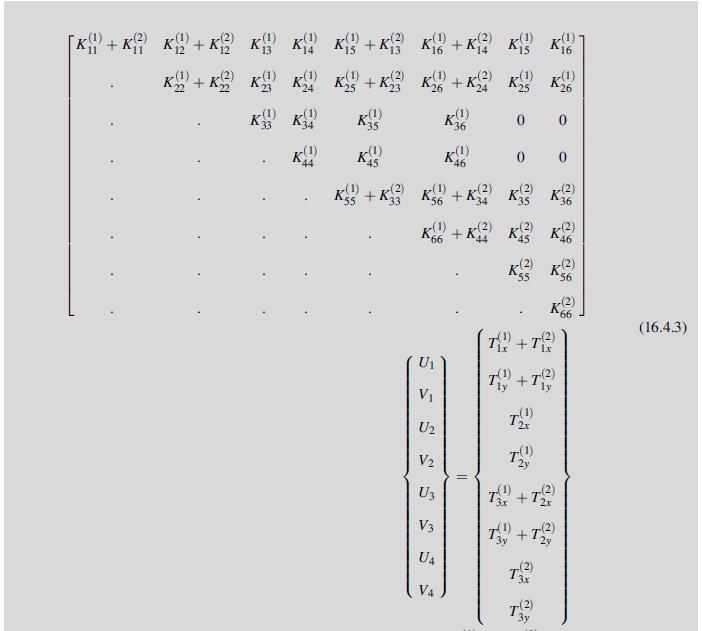
Equation 16.4.1

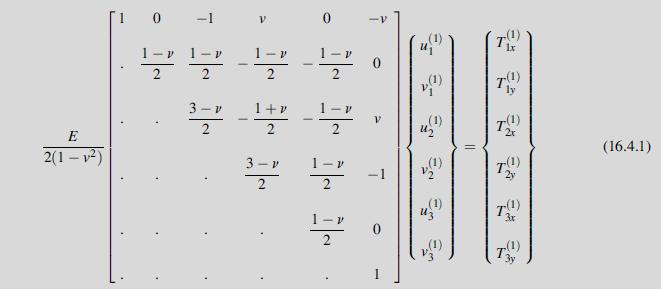
Equation 16.4.2

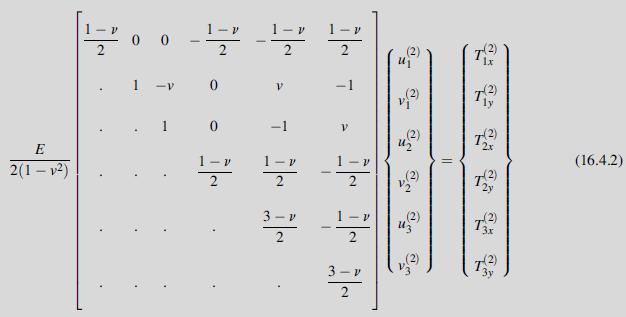
Transcribed Image Text:

Consider the plane stress problem of an isotropic elastic plate under uniform tension with zero body forces, as shown in Fig. 16.3. For convenience, the plate is taken with unit dimensions and thickness and is discretized into two triangular elements as shown. This simple problem is chosen in order to demonstrate some of the basic FEM solution procedures previously presented. More complex examples are discussed in the next section to illustrate the general power and utility of the numerical technique.