For the mode III crack problem in Exercise 8.44, explore the strain energy in a circular area of radius R centered at the crack tip. Refer to the discussion in Section 5.8 and use relation (6.1.10) to explicitly determine the strain energy. Comment on whether the expression is singular or not as R→0.

Data from exercise 8.44

Consider the crack problem shown for the anti-plane strain case with u = v = 0, w = w(x,y). From Section 7.4, the governing equation for the unknown displacement component with zero body force was given by Laplace’s equation, which in polar coordinates reads.

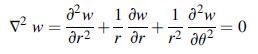
Equation 6.1.10

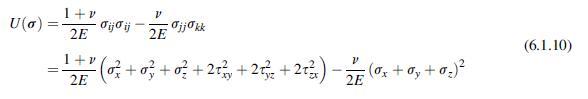
Data from section 5.8

Before leaving this chapter, we wish to briefly discuss a somewhat unpleasant feature of our elasticity model. In later chapters we will find that some generated solutions will have particular singularities that result in unbounded and/or discontinuous stress and displacement predictions. These types of solutions normally come from problems that contain some form of singularity or discontinuity in the geometry and/or boundary conditions. Such problems commonly have geometries that include sharp corners, notches or cracks. Some cases include problems with various point or concentrated loadings, while other examples come from dislocation modeling where there is specification of particular displacement discontinuities. Fig. 5.13 illustrates some of these typical examples, and these particular cases will be formally analyzed in later chapters. Fortunately, much of these unbounded predications are generally localized to regions near the discontinuous boundary or loading as shown in shaded gray areas in the figure. This type of solution behavior should not be surprising since our elasticity model is based on mathematical principles from continuum mechanics field theory. Such theories assume continuous distributions of mass and field variables at all length scales. While such assumptions allow the development of elegant theoretical models, they do not take into account real materials and real geometry which have microstructure. For example, actual materials are composed of atoms, molecules, grains, etc., and thus are not continuous at small length scales. Likewise, real structures do not have infinitely sharp corners, notches or cracks, and loadings can never be truly concentrated at a point. Furthermore, we know that all materials have a finite stress or displacement limit that if exceeded will

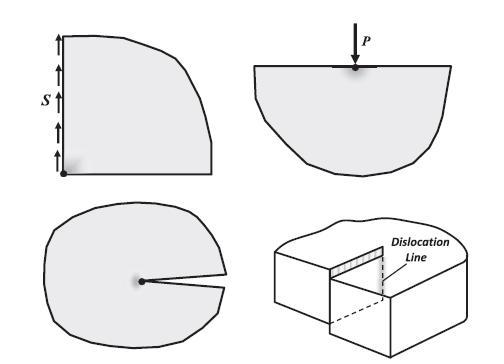
result in non-elastic failure behavior. All of this implies that such unbounded elastic behaviors coming from these types of problems have to be viewed as approximations. There has been considerable research to develop higher order theories in an attempt to remove these unpleasant features of classical elasticity theory. We will further explore some of these in Chapter 15. Some authors (Barber, 2010) have suggested an allowable singularity criterion based on stored strain energy (covered in detail in Chapter 6). The proposed criterion is that the only acceptable singularities are those for which the total strain energy in a small region surrounding the singular point vanishes as the region’s size shrinks to zero. As will be shown, the total strain energy UT in region V is given by the integral

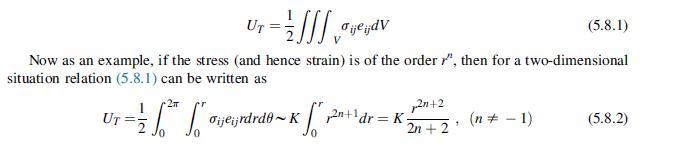
where K is a constant coming from terms that depend on elastic constants and the stress-strain distribution with respect to angle θ .  We therefore conclude that the proposed criterion for an acceptable singularity would require 2n + 2 > 0 ⇒ n >–1. Note that this restriction is not always satisfied by various exact elasticity solutions. For example, the singular crack problem example field given by (8.4.56) does satisfy the energy criterion, but the Flamant solution given by relation (8.4.34) does not. Hence although this energy criterion makes some physical sense, it is not a rigid rule when dealing with elasticity singularity problems.

Transcribed Image Text:

D 10w + = + 2 20 r r aw 1 dw dr2 0