Consider the crack problem shown for the anti-plane strain case with u = v = 0, w

Question:

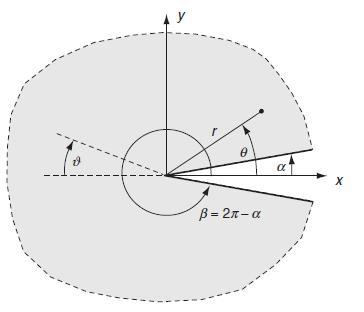
Consider the crack problem shown for the anti-plane strain case with u = v = 0, w = w(x,y). From Section 7.4, the governing equation for the unknown displacement component with zero body force was given by Laplace’s equation, which in polar coordinates reads.

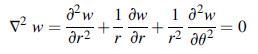
7 aw 1 dw + r r dr 1 3 w ar 30 0

Use a separation of variables scheme with w = f (0), where is a parameter to be determined and f (0) is

Data from section 8.4.10

Consider the original wedge problem shown in Fig. 8.16 for the case where angle a is small and is 2 - . This

0 B = 2- X

while the identical conditions at 0=6=27- = 2 produce sin 2 (2 2) ^ 2 si - sin 272C +[cos 2(2-2) - cos 2] =

Near the tip of the notch 0 and the stresses will be of order O(2), while the displacements are O(-1). At

$Such relations play an important role in fracture mechanics by providing information on the nature of the$

The remaining constants A and B are determined from the far-field boundary conditions. However, an important

Data from section 7.4

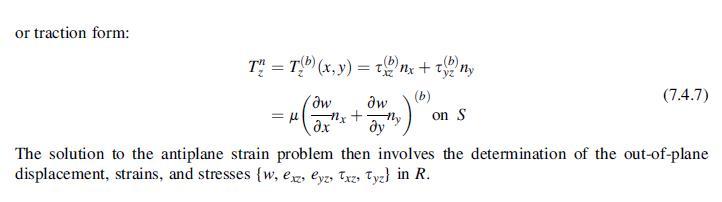
or traction form: T = T(x,y) = tnx + t2ny (b) dw My 1.) the on dy = w nx +. x on S (7.4.7) The solution to

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books

Question Posted: Jan 27, 2024 10:00 PM

See More Questions

Consider the crack problem shown for the anti-plane strain case with u = v = 0, w

Question:

D 10w + = + 2 20 r r aw 1 dw dr2 0

Step by Step Answer:

Using w Ar f0 in Vw0 KKDr Wr hr 0 fK 0 f Solution f Asin 20 B cos 20 Cho...View the full answer

Elasticity Theory Applications And Numerics

Students also viewed these Engineering questions