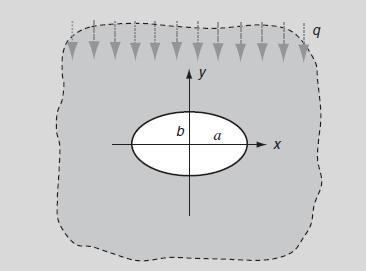
In Example 12 5, show that the dimensionless hoop stress around the boundary of the hole is given by Data from example 12 5 Je e Exqa k For the cases m (1 m) (1 m m) sine msin30 (1 2m cos20 m) 0, 1 2, 1, plot and compare the behaviour of 7 versus 0 (0 0 2) ...

From Example 12 5 the nondimensiona 1 hoop stress around hole ...

In Example 12.5, show that the dimensionless hoop stress around the boundary of the hole is given

Question:

In Example 12.5, show that the dimensionless hoop stress around the boundary of the hole is given by:

Je e Exqa/k For the cases m = (1 +m)[(1 +m+ m) sino - msin30] (1-2m cos20+ m) = 0, 1/2, +1, plot and compare

Data from example 12.5

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books

Question Posted: Jan 15, 2024 05:03 AM

See More Questions

For the elliptical hole problem in Example 12.5, show that by letting m = 0, the stress results will reduce to those of the circular hole problem given in Example 12.4. Data from example 12.5 Data...
The radius Rh and mass Mh of a black hole are related by Rh = 2GMh/c2, where c is the speed of light. Assume that the gravitational acceleration ar of an object at a distance ro = 1.001Rh, from the...
Consider the problem of an infinite plate containing a stress-free elliptical hole with x = y = 0; xy = S. For this problem, the derivative of the complex potential has been developed by...
For the non-seasonal frequencies, use $g \operatorname{lm}()$ to fit the additive exponential model \[ E\left(|\hat{Y}(\omega)|^{2}ight)=\beta_{0}+\beta_{1} \exp \left(-|2 \pi \lambda \omega|^{1 /...
At time t = 0, a ball is struck at ground level and sent over level ground. Figure gives momentum p versus t during the flight (p0 = 6.0 kg m/s and p1 = 4.0 kg m/s). At what initial angle is the ball...
You were in the final stages of your audit of the financial statements of Ozine Corporation for the year ended December 31, 20X2, when you were consulted by the corporations president. The president...
1. Distinguish between job descriptions and job specifications, and explain how they help in selecting employees.
The data file counties.dat contains information on land area, population, number of physicians, unemployment, and a number of other quantities for an SRS of 100 of the 3141 counties in the United...
1 Data Table Laguna Model Construction period Direct materials costs Direct labor costs Direct labor-hours Feb-June 2017 106,440 $ 36,625 $ Mission Model May-Oct 2017 127,250 41,130 1,090 $ 970...
Show that for the plane anisotropic problem, the heat-conduction equation for uncoupled steady-state conditions is given by: Looking for solutions that are of the form T = (x+y), show that this leads...
Plot the isotherms (contours of constant temperature) for Examples 12.4 and 12.5. Data from example 12.5 Data from example 12.4 Similar to the previous example, we now investigate the localized...
The Multigig Computer Corporation is trying to choose between the following two mutually exclusive design projects: a. If the required return is 9 percent and Multigig Computer applies the...
5. Consider the classes below and determine what is printed out by the client code. public class V { public void one(){ System.out.print("it"); } public void two(){ System.out.print("go"); } } public...
Consider the following closed economy short-run IS-LM model with income taxation. The economy is described by equations (1) through (6): (1) C = 200 + 0.8(Y -T); (2) T = 800+0.25Y;(3) G = 500; (4) 1...
(30 pts) A binary search tree is given, write a method to delete a node from the tree. Assume the successor and predecessor methods are provided, partial code is provided below. Finish the reset of...
Reminder: Formatting is always important in your code (comments, indentation, variable names, etc.) And please always start your Java code file with a multi-line comment listing the name of the...
An element is the majority of a size-n array A [1...n] if it occurs more than 1 times in the array. Design a O(log n) time algorithm to find the majority of A in the EREW PRAM model using n...
On the figures, identify which of the curves is a graph of the derivative of the other. 2 5432101
Write a program that initializes an array. It inputs a value from the user and searches the number in the array.
A projectile is launched with a velocity of 100 m/s at an angle of 30) above the horizontal. Create a Simulink model to solve the projectiles equations of motion where x and y are the horizontal and...
The following equation has no analytical solution even though it is linear. x + x = tan t x(0) = 0 The approximate solution, which is less accurate for large values of t, is Create a Simulink model...
Construct a Simulink model to plot the solution of the following equation for 0 t 10. where u s (t) is a unit-step function (in the Block Parameters window of the Step block, set the Step time to...
The number of hours studied and the scores that students earned are shown. Creating a scatter chart, which statement is true regarding the relationship between the hours of study and scores earned....
Five samples of 12 each were extracted from a population. Based on the central limit theorem, what is the best estimate of the SD of the population? A B C D E 270 230 290 238 315 303 274 270 246 244...
In a national test, the mean score was 1575 and the standard deviation was 85. What % of the students earned a score between1500 and 1600 if the scores were Normally distributed?

In Example 12.5, show that the dimensionless hoop stress around the boundary of the hole is given

Question:

Je e Exqa/k For the cases m = (1 +m)[(1 +m+m) sine -msin30] (1-2m cos20+ m) = 0, 1/2, 1, plot and compare the behaviour of 7 versus 0 (0 0 2).

Step by Step Answer:

From Example 12 5 the nondimensiona 1 hoop stress around hole ...View the full answer

Elasticity Theory Applications And Numerics

Students also viewed these Engineering questions