Show that for the plane anisotropic problem, the heat-conduction equation for uncoupled steady-state conditions is given by:

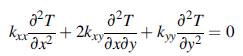
Looking for solutions that are of the form T = (x+λy), show that this leads to the quadratic characteristic equation:

Using the fact that k_xxk_yy > k²
_xy, demonstrate that the two roots to this equation will be complex conjugate pairs; therefore, since the temperature must be real, the final form of the solution will be:

Data from exercise 11.16

Using separation of variables and Fourier methods, solve the conduction equation and verify that the temperature distribution (12.8.20) in Example 12.4 does indeed satisfy insulated conditions on the circular hole and properly matches conditions at infinity.

Transcribed Image Text:

-+kyy ay kxx 2x - + 2 = 0