Using separation of variables and Fourier methods, solve the conduction equation and verify that the temperature distribution
Question:
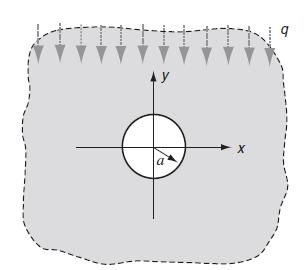
Using separation of variables and Fourier methods, solve the conduction equation and verify that the temperature distribution (12.8.20) in Example 12.4 does indeed satisfy insulated conditions on the circular hole and properly matches conditions at infinity.
Equation 12.8.20
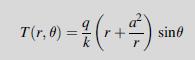
Data from example 12.4



Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.
Question Posted:





