In light of Exercise 2.14 , the compatibility equations (2.6.2) can be expressed as n ij =
Question:
In light of Exercise 2.14 , the compatibility equations (2.6.2) can be expressed as nij = εikl εjmpelp,km = 0, where nij is sometimes referred to as the incompatibility tensor (Asaro and Lubarda, 2006). It is observed that hij is symmetric, but its components are not independent from one another. Since the divergence of a curl vanishes, show that they are related through the differential Bianchi relations nij,j = 0, which can be expanded to:

Thus, we see again that the six compatibility relations are not all independent.
Data from exercise 2.14
Using relation (1.3.5), show that the compatibility relations (2.6.1) with l = k can be expressed by ŋij = εiklεjmpelp,km = 0, which can also be written in vector notation as ∇ × e × ∇ = 0.
Equation 1.3.5
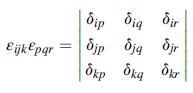
Equation 2.6.1
![]()
Equation 2.6.2
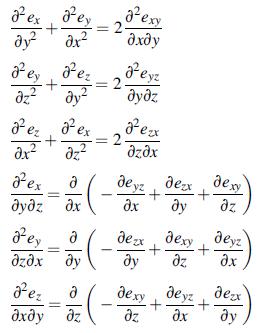
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





