The potentials:

 

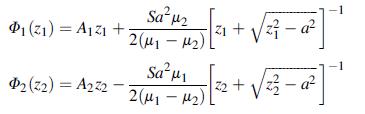
were proposed to solve the plane extension of an anisotropic panel containing a crack of length 2a (see Fig. 11.12). Recall that the constants A₁ and A₂ correspond to the uniform tension case, and for stress S in the y direction:

   Fig 11.12

(a). Determine the general stress field and verify the far-field behavior.
(b). Show that the stress field is singular at each crack tip.
(c). Using the limiting procedures as related to Fig. 10.20, verify that the crack-tip stress field is given by (11.6.10).

Fig 10.20

Equation 11.6.10

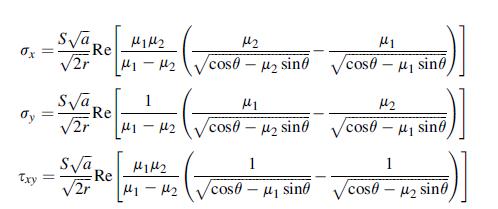
Transcribed Image Text:

P1 (21) A121 + $2(22) = A222 Sa 2 (14 - 14) 1 + / - 0 Sa 2(4 ) 22+2-a L