Under the conditions of polar axis symmetric, verify that the Navier equations (5.4.4) reduce to relation (8.3.10). Refer to Example 1.5 to evaluate vector terms in (5.4.4) properly. Next show that the general solution to this CauchyeEuler differential equation is given by (8.3.11). Finally, use this solution to determine the stresses and show that they will not contain the logarithmic terms given in the general solution (8.3.8).

Data from example 1.5

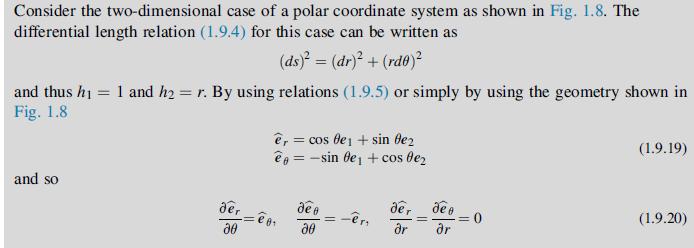
Equation 5.4.4

Equation 8.3.10

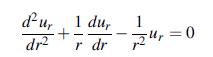
Equation 8.3.11

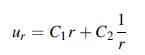
Equation 8.3.8

Transcribed Image Text:

Consider the two-dimensional case of a polar coordinate system as shown in Fig. 1.8. The differential length relation (1.9.4) for this case can be written as (ds) = (dr) + (rd0) and thus h = 1 and h = r. By using relations (1.9.5) or simply by using the geometry shown in Fig. 1.8 and so der 30 er = cos 0e1+ sin 0e2 e sin be + cos 0e 81 deo 30 = -er. der de ar r = = 0 (1.9.19) (1.9.20)