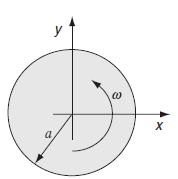
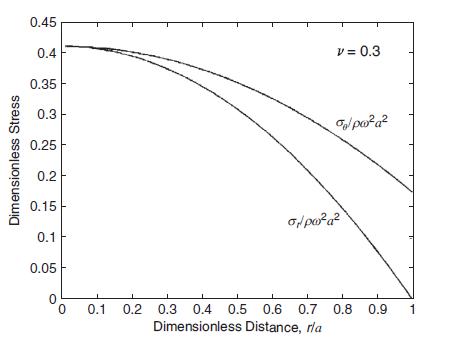
For the rotating disk problem given previously in Example 8.11, the governing equilibrium equation was given by
Question:
For the rotating disk problem given previously in Example 8.11, the governing equilibrium equation was given by (8.4.74). Since this equation is also valid for anisotropic materials, consider the polar-orthotropic case and use equations (11.7.3) to express the equilibrium equation in terms of the displacement as:
Data from example 8.11




Equation 8.4.74
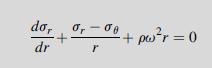
Equation 11.7.3
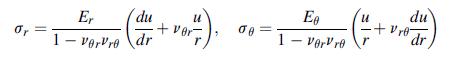
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.
Question Posted:





