Under the stated symmetry conditions in Section 11.7.2, explicitly show that in the absence of body forces the general equilibrium equations reduce to forms (11.7.17) and (11.7.18).
Verify the general displacement solution given by (11.7.19) and (11.7.20), and the particular stress solution (11.7.21) and (11.7.22) for the external loading case.

Data from section 11.7.2

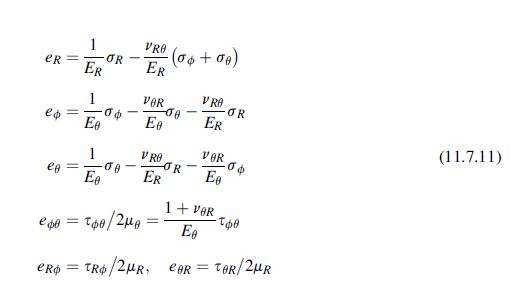
Equation 11.7.17

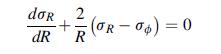
Equation 11.7.18

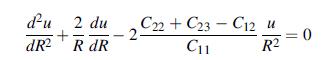Equation 11.7.19

Equation 11.7.20

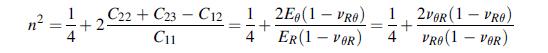
Equation 11.7.21

Equation 11.7.22

Transcribed Image Text:

Following the work of Lekhnitskii (1981) and Horgan and Baxter (1996), we next explore a three- dimensional case using a spherical coordinate system as shown in Fig. B.1. Similar to our previous example, we assume that the material has a uniform microstucture such that properties have orthogonal symmetry with respect to the R, , 0 directions. Under these assumptions, the material would be classified as being spherical-orthotropic. We make one further simplification, and assume that properties in the p and directions are the same. Under these conditions, relation (11.2.10) would allow us to express Hooke's law in the form