Using the MATLAB PDE Toolbox (or equivalent), develop an FEM solution for the torsion of a cylinder
Question:
Using the MATLAB PDE Toolbox (or equivalent), develop an FEM solution for the torsion of a cylinder of circular section with circular keyway as shown in Exercise 9.23. Verify the result of Exercise 9.24, that the maximum shear stress on the keyway is approximately twice that found on a solid shaft. In order to investigate the shear stress, use the Toolbox plot selection window to plot contours of the variable abs(grad(u)).
Data from exercise 9.23
A circular shaft with a keyway can be approximated by the section shown in the following figure. The keyway is represented by the boundary equation r = b, while the shaft has the boundary relation r = 2a cos θ. Using the technique of Section 9.4, a trial stress function is suggested of the form:
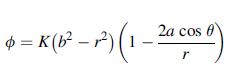
where K is a constant to be determined. Show that this form will solve the problem and determine the constant K. Compute the two shear stress components τ xz and τ yz.
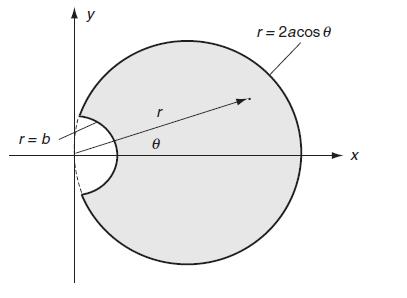
Data from exercise 9.24
For the keyway section of Exercise 9.23, show that resultant stresses on the shaft and keyway boundaries are given by:
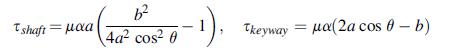
Determine the maximum values of these stresses, and show that for b
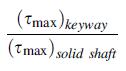
versus the ratio b/a over the range 0≤ b=a≤ 1: Note that (τmax) solid shaft is the maximum shear stress for solid shaft of circular section and can be determined from Example 9.1 or strength of materials theory. Show that the stress concentration plot gives:
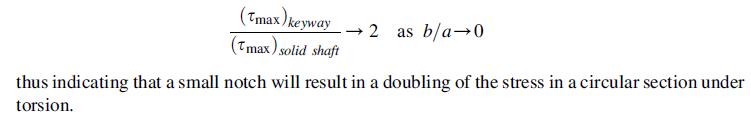
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





