Referring to (3.29), this exercise provides a direct proof that

which is straightforward once the solution is known. Define

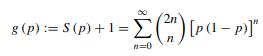
so that

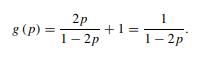
Next, let

so that the relation for S (p) is equivalent to showing that h (p) = 1. Clearly

is zero, so that

Thus, if h (p) = g (p) (1 − 2p) − 2g (p) can be shown to be zero, it follows that h (p) = 1 for all p ∈
0, 1/2) so that, in turn, the proof of the closed-form solution to S (p) is established for all p ∈
0, 1/2). Show that g (p) (1 − 2p) = 2g (p).
(Contributed by Markus Haas)

=l S (p)=(") [p - p)]" = 2p 1-2p P