For the exponential family of distributions defined in (4.41), show (a) (E(y)=frac{d}{d theta} b(theta)). (b) (operatorname{Var}(y)=a(phi) frac{d^{2}}{d
Question:
For the exponential family of distributions defined in (4.41), show
(a) \(E(y)=\frac{d}{d \theta} b(\theta)\).
(b) \(\operatorname{Var}(y)=a(\phi) \frac{d^{2}}{d \theta^{2}} b(\theta)\).
(c) Assume that \(y \sim N\left(\mu, \sigma^{2}\right)\) and \(\sigma^{2}\) is known. Show that the canonical link for the mean \(\mu\) is the identity function \(g(\theta)=\theta\).
(d) Show that the canonical link for Bernoulli distribution is the logistic function.
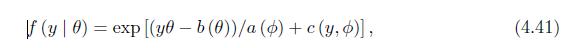
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Applied Categorical And Count Data Analysis
ISBN: 9780367568276
2nd Edition
Authors: Wan Tang, Hua He, Xin M. Tu
Question Posted:





