Construct a 99% confidence interval for the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Los Angeles, California, using the data from Exercise 28.

You can construct a confidence interval for the difference between two population means μ₁ - μ₂, as shown below, when both population standard deviations are known, and either both populations are normally distributed or both n₁ ≥ 30 and n₂ ≥ 30. Also, the samples must be randomly selected and independent.

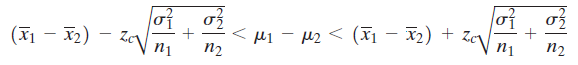
Construct the indicated confidence interval for μ₁ - μ₂.

Data from exercise 28:

Is the difference between the mean annual salaries of entry level architects in Denver, Colorado, and Los Angeles, California, equal to $10,000? To decide, you select a random sample of entry level architects from each city. The results of each survey are shown in the figure. Assume the population standard deviations are σ₁ = $6520 and σ₂ = $7130. At α = 0.01, what should you conclude?

V n1