Binomial probabilities are often hard to compute by hand, because the computation involves factorials and numbers raised to large powers. It can be shown through algebraic manipulation that if X is a random variable whose distribution is binomial with n trials and success probability p, then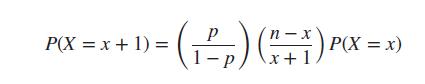

If we know P(X = x), we can use this equation to calculate P(X = x + 1) without computing any factorials or powers.

a. Let X have the binomial distribution with n = 25 trials and success probability p = 0.6. It can be shown that P(X = 14) = 0.14651. Find P(X = 15).

b. Let X have the binomial distribution with n = 10 trials and success probability p = 0.35. It can be shown that P(X = 0) = 0.0134627. Find P(X = x) for x = 1, 2, ..., 10.

P(X = x + 1) = 1-P (+) (+) P(X = x) n-x x+1