Refer to Exercise 19.

Use the normal approximation to estimate the critical values X2 0.025 and X2 0.975 for a 95% confidence interval, and construct a 95% confidence interval for σ.

The chi-square distribution is skewed, but as the number of degrees of freedom becomes large, the skewness diminishes. If the number of degrees of freedom, k, is large enough, the chi-square distribution is reasonably well approximated by a normal distribution with mean k and variance 2k.

Exercise 19

A sample of size 101 from a normal population has sample standard deviation s = 40.

Use Table A.4 to find the exact critical values X2 0.025 and X2 0.975 for a 95% confidence interval, and construct a 95% confidence interval for σ.

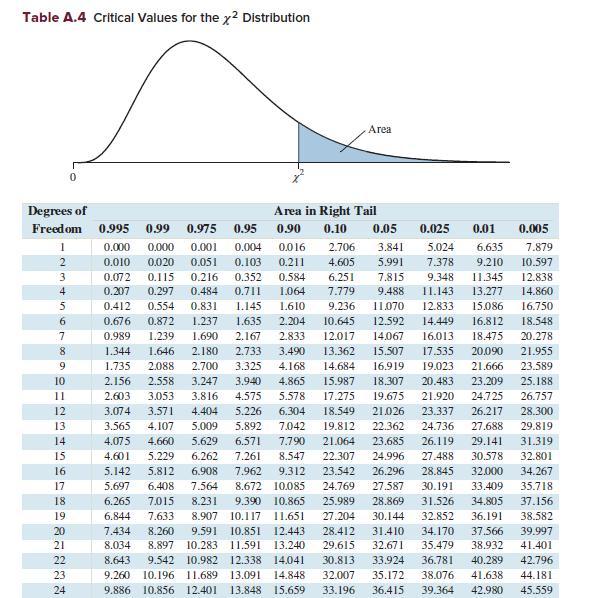
Transcribed Image Text:

Table A.4 Critical Values for the x2 Distribution Area Degrees of Freedom Area in Right Tail 0.995 0.99 0.975 0.95 0.90 0.10 0.05 0.025 0.01 0.005 1 0.000 0.000 0.001 0.004 0.016 2 3 0.072 0.010 0.020 0.115 0.051 0.103 0.216 0.211 0.352 0.584 6.251 2.706 3.841 5.024 6.635 7.879 4.605 5.991 7.378 9.210 10.597 7.815 9.348 11.345 12.838 4 0.207 0.297 0.484 0.711 1.064 7.779 9,488 11.143 13.277 14.860 5 0.412 0.554 0.831 1.145 1.610 9.236 11.070 12.833 15.086 16.750 6 0.676 0.872 1.237 1.635 2.204 10.645 12.592 14.449 16.812 18.548 7 0.989 1.239 1.690 2.167 2.833 12.017 14.067 16.013 18.475 20.278 8 1.344 1.646 2.180 2.733 3.490 13.362 9 1.735 2.088 2.700 3.325 10 2.156 2.558 3.247 3.940 4.168 4.865 11 2.603 3.053 3.816 4.575 5.578 12 3.074 3.571 4.404 5.226 6.304 18.549 13 3.565 4.107 5.009 5.892 7.042 19.812 14 4.075 15 4.601 16 17 18 283232 19 20 21 24 4.660 5.629 6.571 5.229 6.262 7.261 8.547 5.142 5.812 6.908 7.962 9.312 5.697 6.408 7.564 8.672 10.085 6.265 7.015 8.231 9.390 10.865 6.844 7.633 8.907 10.117 11.651 7.434 8.260 9.591 10.851 12.443 8.034 8.897 10.283 11.591. 13.240 8.643 9.542 10.982 12.338 14.041 9.260 10.196 11.689 13.091 14.848 9.886 10.856 12.401 13.848 15.659 7.790 21.064 28.412 15.507 17.535 20.090 14.684 16.919 19.023 21.666 23.589 15.987 18.307 20.483 23.209 25.188 17.275 19.675 21.920 24.725 26.757 21.026 23.337 26.217 28.300 22.362 24.736 27.688 29.819 23.685 26.119 29.141 31.319 22.307 24.996 27.488 30.578 32.801 23.542 26.296 28.845 32.000 34.267 24.769 27.587 30.191 33.409 35.718 25.989 28.869 31.526 34.805 37.156 27.204 30.144 32.852 36.191 31.410 34.170 21.955 38.582 37.566 39.997 29.615 32.671 35.479 38.932 41.401 30.813 33.924 32.007 35.172 33.196 36.781 40.289 42.796 38.076 41.638 44.181 36.415 39.364 42.980 45.559