The following table is a life table, reproduced from the chapter introduction. With an understanding of some
Question:
The following table is a life table, reproduced from the chapter introduction. With an understanding of some basic concepts of probability, one can use the life table to compute the probability that a person of a given age will still be alive a given number of years from now. Life insurance companies use this information to determine how much to charge for life insurance policies.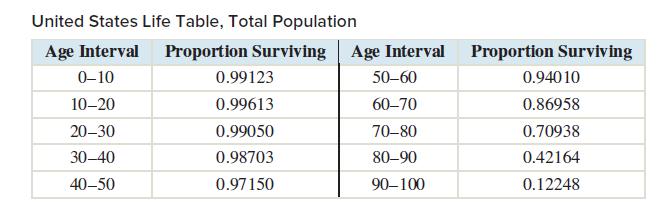
The column labeled ‘‘Proportion Surviving’’ gives the proportion of people alive at the beginning of an age interval who will still be alive at the end of the age interval. For example, among those currently age 20, the proportion who will still be alive at age 30 is 0.99050, or 99.050%. We will begin by computing the probability that a person lives to any of the ages 10, 20, ... , 100.
The first number in the column is the probability that a person lives to age 10. So![]()
The key to using the life table is to realize that the rest of the numbers in the ‘‘Proportion Surviving’’ column are conditional probabilities. They are probabilities that a person is alive at the end of the age interval, given that they were alive at the beginning of the age interval. For example, the row labeled ‘‘20–30’’ contains the conditional probability that someone alive at age 20 will be alive at age 30:![]()
Compute the probability that a person lives to a given age.
1. From the table, find the conditional probability P (Alive at age 20 | Alive at age 10).
2. Use the result from Exercise 1 along with the result P (Alive at age 10) = 0.99123 to compute P (Alive at age 20).
3. Use the result from Exercise 2 along with the appropriate number from the table to compute P (Alive at age 30).
4. Use the result from Exercise 3 along with the appropriate number from the table to compute P (Alive at age 40).
5. Compute the probability that a person is alive at ages 50, 60, 70, 80, 90, and 100.
In Exercises 1–5, we computed the probability that a newborn lives to a given age. Now let’s compute the probability that a person aged x lives to age y. We’ll illustrate this with an example to compute the probability that a person aged 20 lives to age 100. This is the conditional probability that a person lives to age 100, given that the person has lived to age 20.
We want to compute the conditional probability![]()
Using the definition of conditional probability, we have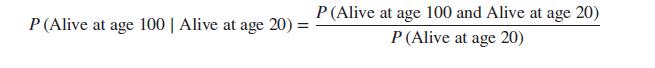
You computed P (Alive at age 20) in Exercise 2. Now we need to compute P (Alive at age 100 and Alive at age 20). The key is to realize that anyone who is alive at age 100 was also alive at age 20. Therefore,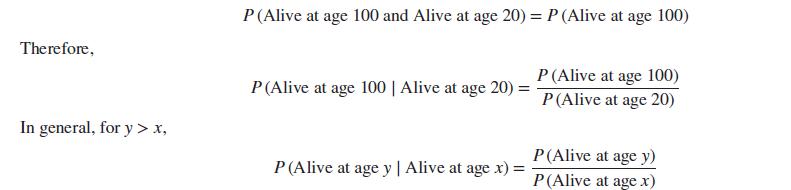
6. Find the probability that a person aged 20 is still alive at age 100.
7. Find the probability that a person aged 50 is still alive at age 70.
8. Which is more probable, that a person aged 20 is still alive at age 50, or that a person aged 50 is still alive at age 60?
9. A life insurance company sells term insurance policies. These policies pay $100,000 if the policyholder dies before age 70, but pay nothing if a person is still alive at age 70. If a person buys a policy at age 40, what is the probability that the insurance company does not have to pay?
Step by Step Answer:






