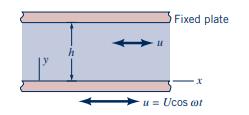
A viscous fluid is contained between wide, parallel plates spaced a distance \(h\) apart as shown in Fig. P7.83. The upper plate is fixed, and the bottom plate oscillates harmonically with a velocity amplitude \(U\) and frequency \(\omega\). The differential equation for the velocity distribution between the plates is

\[ ho \frac{\partial u}{\partial t}=\mu \frac{\partial^{2} u}{\partial y^{2}} \]

where \(u\) is the velocity, \(t\) is time, and \(ho\) and \(\mu\) are fluid density and viscosity, respectively. Rewrite this equation in a suitable nondimensional form using \(h, U\), and \(\omega\) as reference parameters.

Figure P7.83

h Fixed plate u = Ucos cot