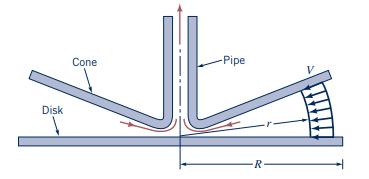
Air flows into a pipe from the region between a circular disk and a cone as shown in Fig. P4.52. The fluid velocity in the gap between the disk and the cone is closely approximated by \(V=V_{0} R^{2} / r^{2}\), where \(R\) is the radius of the disk, \(r\) is the radial coordinate, and \(V_{0}\) is the fluid velocity at the edge of the disk. Determine the acceleration for \(r=0.5\) and \(2 \mathrm{ft}\) if \(V_{0}=5 \mathrm{ft} / \mathrm{s}\) and \(R=2 \mathrm{ft}\).

Figure P4.52

Disk Cone -Pipe R-