Air flows steadily through a converging-diverging rectangular channel of constant width as shown in Fig. 3.85 and

Question:

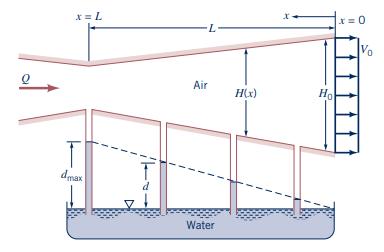
Air flows steadily through a converging-diverging rectangular channel of constant width as shown in Fig. 3.85 and Video V3.10. The height of the channel at the exit and the exit velocity are \(H_{0}\) and \(V_{0}\) respectively. The channel is to be shaped so that the distance, \(d\), that water is drawn up into tubes attached to static pressure taps along the channel wall is linear with distance along the channel. That is \(d=\left(d_{\max } / \mathrm{L}\right) x\), where \(L\) is the channel length and \(d_{\max }\) is the maximum water depth (at the minimum channel height: \(x=L)\). Determine the height, \(H(x)\), as a function of \(x\) and the other important parameters.

Figure P3.85