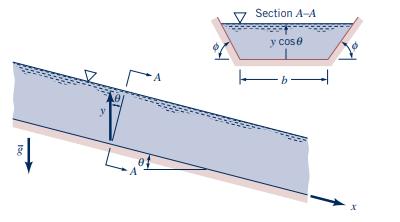
Consider the flow down a prismatic channel having a trapezoidal cross section of base width \(b\) and top width \(b+2 y\) \(\cos \theta \cot \phi\). The channel bottom makes an angle \(\theta\) with the horizontal, and \(y\) is the vertical fluid depth. (See Fig. P11.71.) Show that

\[ \frac{d y}{d x}=\frac{\tan \theta-\left(n^{2} Q^{2} / A^{2} R_{h}^{4 / 3} \kappa^{2}\right)}{1-\left[\frac{Q^{2}}{A^{2} g y \cos ^{2} \theta}\right]\left[\frac{b+2 y \cos \theta \cot \phi}{b+y \cos \theta \cot \phi}\right]} \]

Note that the average fluid velocity is given by

\[ V=\frac{Q}{A}=\frac{Q}{y \cos \theta(b+y \cos \theta \cot \phi)} \]

Discuss the form of the equation for small values of \(\theta\left(\theta \sim 1^{\circ}\right)\).

Figure P10.71

100 Section A-A y cose