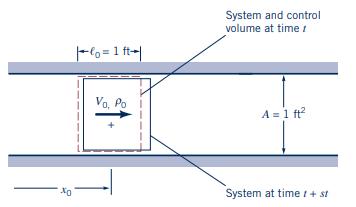
Figure P4.64 shows a fixed control volume. It has a volume \(V_{0}=1.0 \mathrm{ft}^{3}\), a flow area \(A=1.0 \mathrm{ft}^{2}\), and a length \(\ell_{0}=1.0 \mathrm{ft}\). Position \(x\) represents the center of the control volume where the fluid velocity \(V_{0}=1.0 \mathrm{ft} / \mathrm{s}\) and the density \(ho_{0}=1.800 \mathrm{slug} / \mathrm{ft}^{3}\). Also, at position \(x\) the fluid density does not change locally with time but decreases in the axial direction at the linear rate of \(0.25 \mathrm{slug} / \mathrm{ft}^{4}\). Use the system or Lagrangian approach to evaluate \(d p / d t\). Compare this result with that of the material derivative and flux terms.

Figure P4.64

Transcribed Image Text:

lo=1 ft- System and control volume at time Vo, Po A = 1 ft System at time + st